Week 4: Binary Search
===========
Binary Search(二元搜尋法)
-------------------------
說明：
一種在有序陣列中尋找某一特定元素的搜尋演算法，原理為將欲搜尋的值，與所有資料的中間值(中位數)做比對。
##步驟
1. 資料需依大小先排序好
2. Middle = ⌊(Left + Right)/2⌋
3. 將鍵值key與搜尋範圍的中間資料data[Middle]作比對
key = data[Middle]：找到
key < data[Middle]：縮小搜尋範圍 ⇒ Right = Middle-1
key > data[Middle]：縮小搜尋範圍 ⇒ Left = Middle+1
4. 重複上步驟，直到找到資料或搜尋範圍交叉(找不到)
##舉例
從排序好的陣列中，找出小於 34的最大值
:
Index of mid = (L+R+1)/2 = (0+14+1)/2 = 7
:
判斷mid有沒有小於34 => 沒有，找左半部
:
Index of mid = (L+R+1)/2 = (0+6+1)/2 = 3
:
判斷mid有沒有小於34 => 有，找右半部
:
Index of mid = (L+R+1)/2 = (4+6+1)/2 = 5
:
判斷mid有沒有小於34 => 沒有，找左半部
:
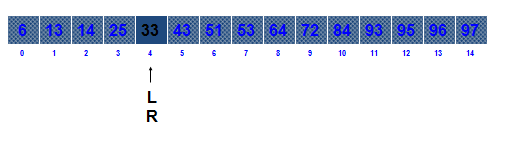
小於34的最大值 = 33
:
##實作
```c++
#include
int binary_search(int *numbers, int n, int val) {
int left = 0, right = n - 1;
while(left < right) {
int middle = (left + right) / 2;
if (numbers[middle] < val) {
left = middle + 1;
} else {
right = middle - 1;
}
}
return right;
}
int main() {
int array[] = {6, 13, 14, 25, 33, 43, 51, 53, 64, 72, 84, 93, 95, 96, 97};
printf("%d\n", binary_search(array, 15, 34)); // 10 50 60
return 0;
}
```
##時間複雜度
T(n) = T(n/2) + Ο(1) = Ο(lgn)