定義
-------------------------------
dynamic programming (also known as dynamic optimization)  is a method for solving a complex problem by breaking it down into a  collection of simpler subproblems, solving each of those subproblems  just once, and storing their solutions - ideally, using a memory-based  data structure<br>
[Reference](https://en.wikipedia.org/wiki/Dynamic_programming)<br><br>

> DP全名為 Dynamic Programming (動態規劃) ，將問題切分多個子問題，簡化問題的複雜度，最後將所以子問題合併得到解答。

特性
---------------------------------
If the problem also shares an [optimal substructure](https://en.wikipedia.org/wiki/Optimal_substructure) property, [dynamic programming](https://en.wikipedia.org/wiki/Dynamic_programming) is a good way to work it out.<br>
[Reference](https://en.wikipedia.org/wiki/Overlapping_subproblems)<br>

> DP的題目有兩個重要的特性
> 1. Optimal Substructure (最佳子問題)
> 2. Overlapping Subproblem(子問題重疊)
<br>
> Q. Why memorization is ineffective in speed up a good divide-and-conquer algorithm such as MERGE_SORT ?
> 
> sol) 
> without overlapping. 如果沒有重疊的子問題，我們會發現時間複雜度並不會因為使用DP而降低，這是因為每次的子問題並沒有重複得部份！

> Example

Coin Change (錢幣交換)
-----------
**想法**

> dp[i]：i 價位是否可以湊的 (false/true)
> v[k]：第k種硬幣
> 
> 如果i-v[k]價位可以湊得，那麼i必定也可以湊得 
> If (dp[ i – v[k] ] == true) dp[ i ] = true;

**每種硬幣數量的差異**<br>

<ol>
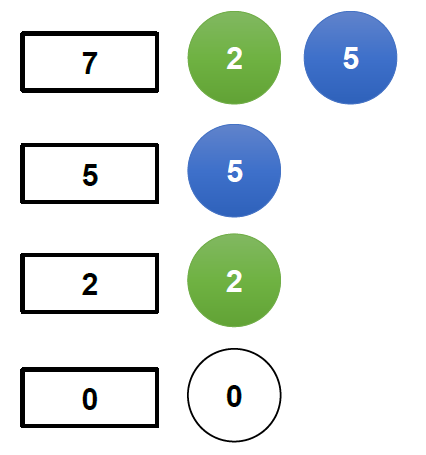
<li> 1 個硬幣</li>

+ dp 的 index 由大到小掃過進行更新。

+ 圖示：N = 1，意即每個硬幣有 1 個。

<br>![](/coin_changing_1_1.png)
<br>![](/coin_changing_1_2.png)

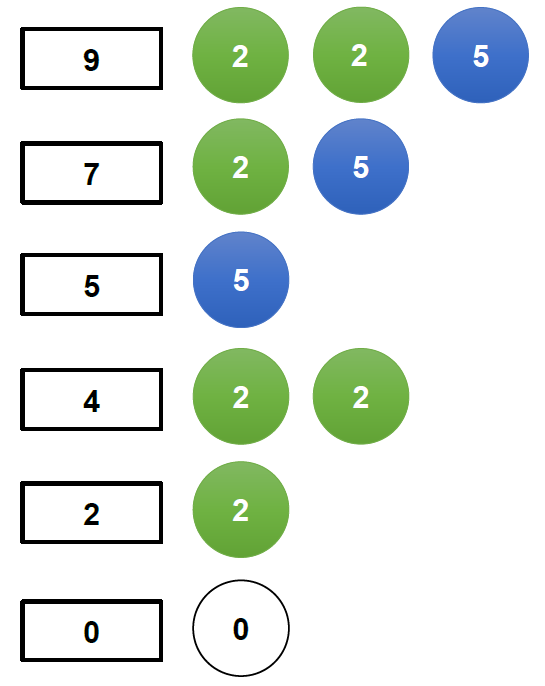
<li> N 個硬幣</li>

+ dp 的 index 由大到小 N 次

+  圖示：假設 N = 2，意即每個硬幣有 2 個。

<br>![](/coin_changing_n_1.png)
<br>![](/coin_changing_n_2.png)

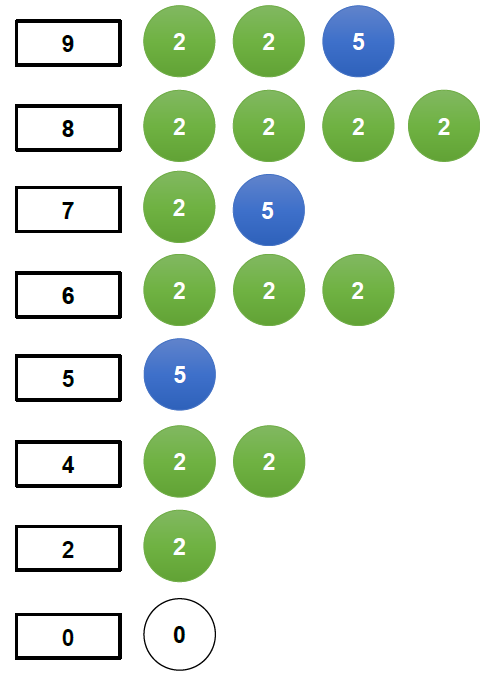
<li>無限硬幣</li>

+ dp 的 index 由小到大掃過進行更新。

+ 圖示：硬幣有無限多個。

<br>![](/coin_changing_inf_1.png)
<br>![](/coin_changing_inf_2.png)

</ol>

**如果題目為湊得該價位有幾種方法，dp所紀錄的是方法數，dp[0]為1，不斷累加方法數到i==該價位**<br>

> If (dp[ i - v[k] ] == true) dp[ i ] += dp[ i - v[k] ];


0/1 Knapsack Problem (0-1背包問題)
-------------
> Knapsack Problem:背包問題
> 將一堆物品塞進背包,要使背包裡的物品總價值最高,但背包有耐重限制,所以塞的太重的話,背包就會撐破。
> 
> 0/1:
> 物品只會放進背包0個或1個,物品不可切割,所以只有不放或者全放兩種可能。
<br>

**想法**<br>

> dp[m]：在m重量下目前的最佳價值
> v[i]：物品i的價值
> w[i]：物品i的重量

**類似硬幣交換的作法，不過dp[m]所紀錄的是目前使用i種物品在m重量可以得到的最佳價值，當發現某物品在相同重量下可以創造更佳的價值就進行更新**

> dp[m] = max( dp[m], dp[m - w[i]] + v[i] ); *

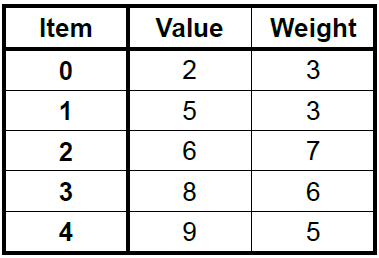
**圖示**
<br>![](/knapsack_problem_2.png)
<br>![](/knapsack_problem_1.png)

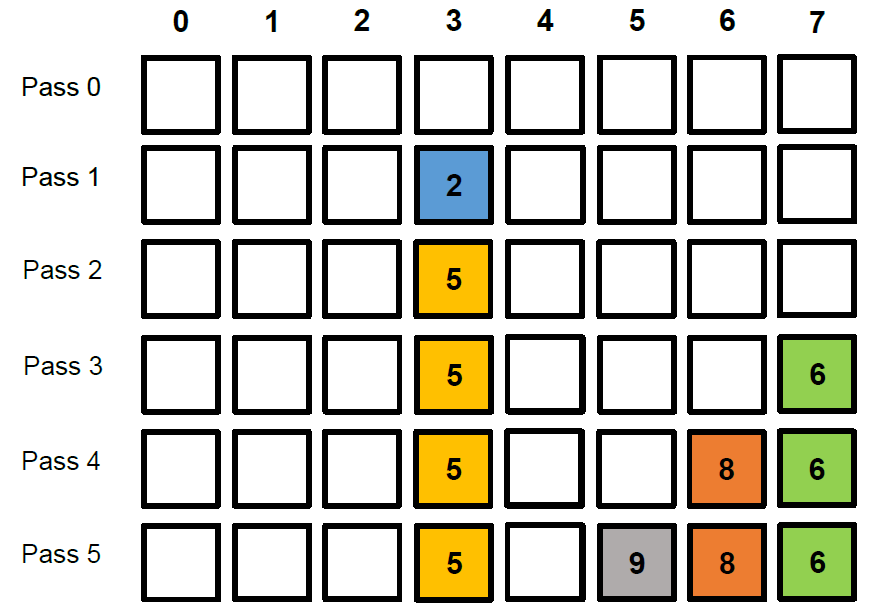
DP v.s Greedy Algorithm
============================

> Greedy 相較 DP 多出一個性質 - Greedy Choice，即每次只要挑選最佳的選擇，最後必定可以得到最佳解。
> 如果今天一件物品可以任意分割成數份，此問題變成為fractional背包問題，因為沒有最後一個物品塞不下的問題，每次只要挑選最高性價比(CP值)的物品，最終一定可以達到最高價值。
> 此問題與0/1背包問題差別就在於fractional背包問題有Greedy Choice特性，因此可以用速度更快的Greedy Algorithm來得到解。