#MST(Minimum Spanning Tree, 最小生成樹)
##Spanning Tree(生成樹)
1. 一棵<b>包含圖上所有點</b>的樹,稱作該圖的<b>生成樹</b>
2. 一張圖的生成樹可能會有很多種
3. <b>完全連通圖</b>才有生成樹(不連通時,則稱為生成森林)
4. 生成樹的權重為樹上每條邊的權重總和
##Minimum Spanning Tree
擁有<b>最小權重</b>的生成樹,稱為最小生成樹
###Kruskal’s algorithm(greedy based)
1. 依照權重排序
2. 選擇較小的邊,並邊檢查是否有迴圈
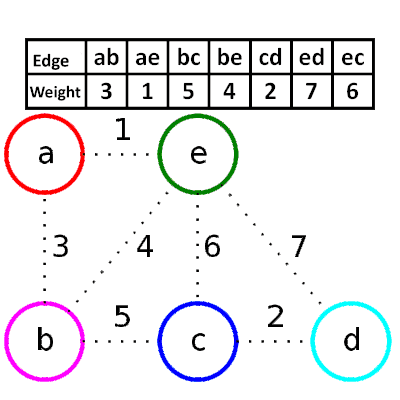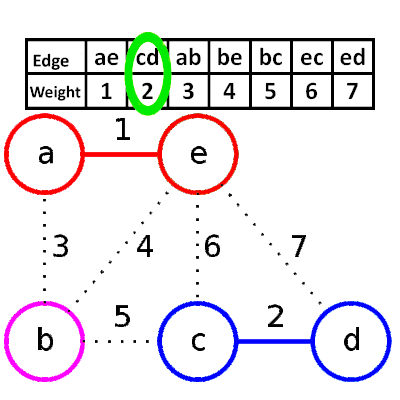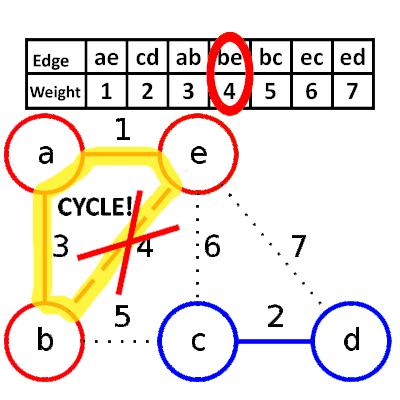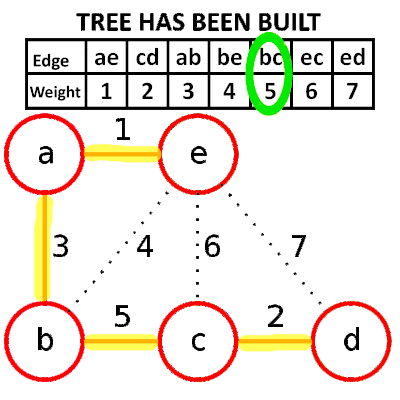
* Psuedocode
totalcost← 0
for each v ∈ V
do MAKE-SET (v)
sort the edges into non-decreasing order by weight
for each edge (u, v) ∈ E, taken in non-decreasing order
do if FIND-SET (u) ≠ FIND-SET (v)
then UNION (u, v)
totalcost← totalcost+ w(u, v)
return totalcost
* 時間複雜度O(ElgE)
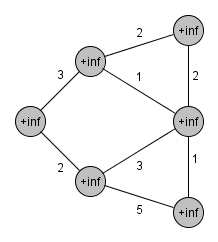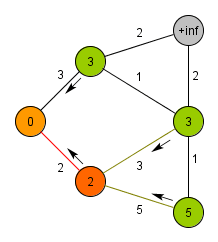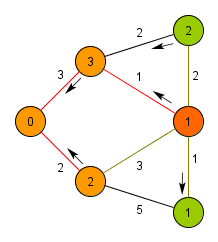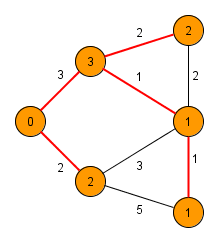
###Prim’s algorithm(relaxation based)
1. 所有節點設為<b>未拜訪</b>過
2. 令d[i]為到節點i的目前距離,起使皆設為INF
3. 每次都去找未拜訪過的節點i,而且d[i]最小
4. 找完後要更新未拜訪過的節點距離d[j]
<b>if(找到的節點i到節點j的距離 < d[j]) 則更新d[j]</b>
```c++
#include <cstdio>
using namespace std;
int main()
{
}
```