acm/course/LINE_Intersection
Week 15: LINE_Intersection
Computational Geometry
Q:我們要學什麼?
A:為了讓電腦幫我們運算幾何問題,學習如何將問題表示為電腦看得懂的樣子。
Struct
基本的幾何形狀有三大要素,點、線、面。
###點 平面中一個點(x,y)
###線 平面中一條線段,可以有許多不同的表示法。
兩點式:紀錄直線上任意兩點,即可表一直線。
點斜式:紀錄直線上任意一點,以及直線的斜率,即可表一直線。
###面 空間中一個平面,可以有許多不同表示法。
紀錄平面上不共線三點,即可表一平面。
紀錄平面的法向量,以及通過平面上一點,即可表一平面。
Vector
資料結構與點相同
向量可以用來進行多種運算
Ex:加、減、乘、除、內 積、外積、夾角等。
程式:
typedef Point Vector;
Vector operator + (Vector A,Vector B) { return Vector(A.x+B.x,A.y+B.y); }
Vector operator - (Point A,Point B) { return Vector(A.x-B.x,A.y-B.y); }
Vector operator * (Vector A,double p) { return Vector(A.x*p,A.y*p); }
Vector operator / (Vector A,double p) { return Vector(A.x/p,A.y/p); }
bool operator < (const Point &A,const Point &B){
return A.x < B.x || (A.x == B.x && A.y < B.y); }
int dcmp (double x){
if (fabs(x)<eps) return 0;
else return x < 0 ? -1 : 1;
}
bool operator == (const Point &A, const Point &B){
return dcmp(A.x-B.x) == 0 && dcmp(A.y-B.y) == 0; }
double Dot(Vector A,Vector B) { return A.x*B.x + A.y*B.y; }
double Length(Vector A) { return sqrt (Dot(A,A)); }
double dis_2p(Point A,Point B) {
return sqrt((double)((A.x-B.x)*(A.x-B.x) + (A.y-B.y)*(A.y-b.y)));
}
double Angle(Vector A,Vector B){
return acos( Dot(A,B)/Length(A)/Length(B) );
}
double Cross(Vector A,Vector B){ return A.x*B.y-A.y*B.x; }###加法 相同座標的項相加。
###減法 相同座標的項相減。
###乘法 所有座標的項乘一常數。
###除法 所有座標的項除一常數。
###小於 從最左邊的座標開始比,輸出最小的。
###全等 所有座標的項都一樣。
int dcmp (double x){
if (fabs(x)<eps) return 0;
else return x < 0 ? -1 : 1;
}
bool operator == (const Point &A, const Point &B){
return dcmp(A.x-B.x) == 0 && dcmp(A.y-B.y) == 0; }###內積 兩向量內積
###外積 兩向量外積
###長度 向量長度
###角度 兩向量間的夾角
Cross
###兩向量順逆時針的方向 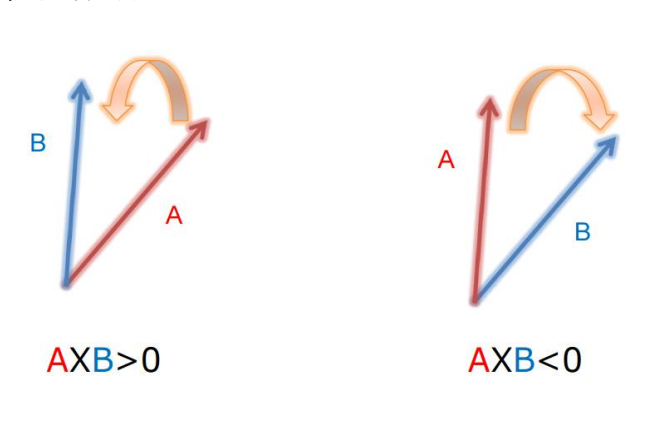
###多邊形面積
double polygon_area(Polygon input){
double A=0;
for(int i=0;i<input.num;i++)
A+=Cross(input.p[i],input.p[i+1]);
return fabs(A/2);
}###點到直線的距離 >公式解
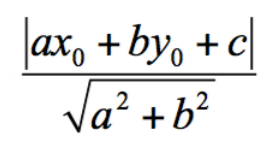
Segment
用兩點式來判斷線段相交情形
int in_interval(Point P1,Point P2,Point P3){
// check if p3 is between p1 p2 return 1 yes 0 no
Point min,max;
if(P1.x>P2.x)min.x=P2.x,max.x=P1.x;
else min.x=P1.x,max.x=P2.x;
if(P1.y>P2.y)min.y=P2.y,max.y=P1.y;
else min.y=P1.y,max.y=P2.y;
if(min.x<=P3.x&&P3.x<=max.x&&min.y<=P3.y&&P3.y<=max.y)return 1;
else return 0;
}
int segments_intersect(Point A,Point B,Point C,Point D){
//check if segment AB CD has intersection return 1 yes 0 no
double d1=Cross( A-C , D-C );
double d2=Cross( B-C , D-C );
double d3=Cross( C-A , B-A );
double d4=Cross( D-A , B-A );
if(dcmp(d1*d2)<0 && dcmp(d3*d4)<0) return 1;
if( dcmp(d1)==0 && in_interval(C,D,A)==1 )return 1;
if( dcmp(d2)==0 && in_interval(C,D,B)==1 )return 1;
if( dcmp(d3)==0 && in_interval(A,B,C)==1 )return 1;
if( dcmp(d4)==0 && in_interval(A,B,D)==1 )return 1;
return 0;###相交 >正常情況下

A和B在異側,C和D也在異側
A和B在異側 : CA Cross CD 和 CB Cross CD 異號
C和D在異側 : AC Cross AB 和 AD Cross AB 異號
例外
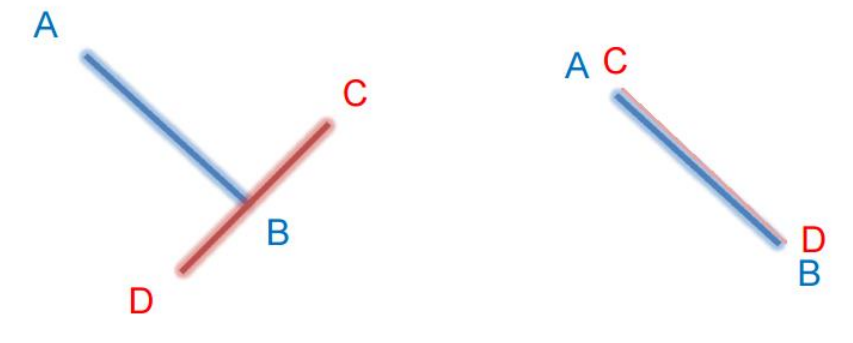
交點重疊或線段重疊
CB Cross CD = 0 且 B要在CD內
B要在CD內 : B的x/y介於C和D的x/y 之間
