acm/course/MST

#MST(Minimum Spanning Tree, 最小生成樹) ##Spanning Tree(生成樹) 1.一棵包含圖上所有點的樹，稱作該圖的生成樹

2.一張圖的生成樹可能會有很多種

3.完全連通圖才有生成樹(不連通時，則稱為生成森林)

4.生成樹的權重為樹上每條邊的權重總和

##Minimum Spanning Tree 擁有最小權重的生成樹，稱為最小生成樹

###Kruskal’s algorithm(greedy based) 1.依照權重排序

2.選擇較小的邊，並邊檢查是否有迴圈 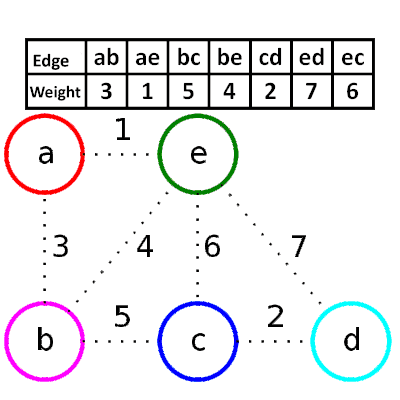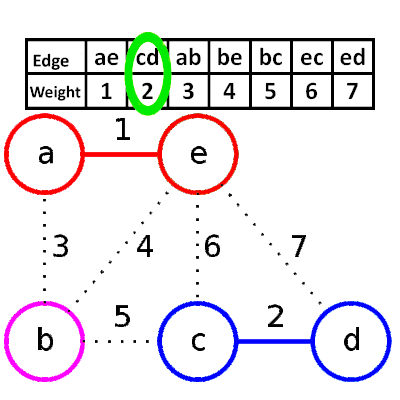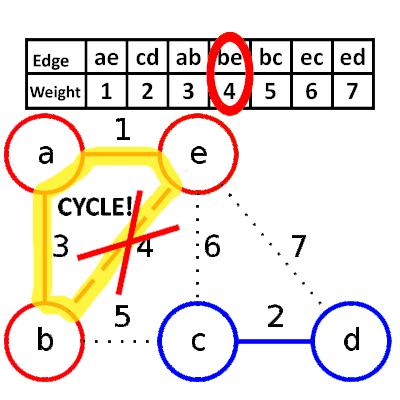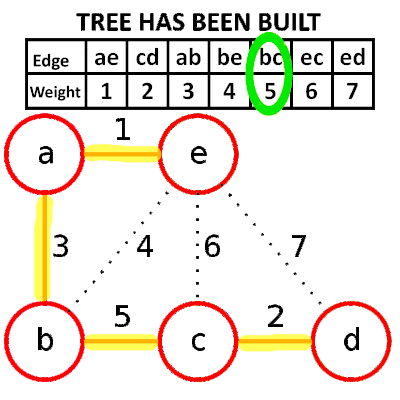* Psuedocode

    totalcost← 0 
    for each v ∈ V
        do MAKE-SET (v)
    sort the edges into non-decreasing order by weight
    for each edge (u, v) ∈ E, taken in non-decreasing order
        do if FIND-SET (u) ≠ FIND-SET (v)
            then UNION (u, v) 
                totalcost← totalcost+ w(u, v)
    return totalcost
* 時間複雜度O(ElgE)

###Prim’s algorithm(relaxation based)

#include <cstdio>
using namespace std;
int main()
{
}