Review 1

I/O

標準的輸入輸出有下列幾種指令

輸入:

scanf, gets, getchar, cin……

輸出:

printf, puts, putchar, cout….

但在比賽時由於需考慮效能所以多使用 scanf, printf 取代cin , cout

(因為cin, cout會回去呼叫scanf, printf)

比賽時常見的題型:

1.給測資的數量

Ex:

A+B problem

int tc,a,b;
scanf("%d",&tc);
while(tc--) {
scanf("%d%d",&a,&b);
printf("%d\n",a+b);
}

2.以特定值(通常為 0)為中止條件

Ex:

Hi, input #

/* Until zero */

int n;
while(scanf("%d",&n)==1 && n) {
printf("Hi, %d.\n",n);
}

3.以EOF(End of file)為中止條件

Ex:

Hi, input #

/* Until EOF */

int n;
while(scanf("%d",&n)!=EOF) {
printf("Hi, %d.\n",n);
}

若題目為指定測資終止條件，則以EOF作為終止條件

Ex:

scanf

while(scanf()!=EOF)
{
     ...
}

fgets

while(gets()!=0)
{
     ...
}

cin

while(cin >> x)
{
     ...
}

1.在每個輸出後面加一個空白行

Ex:

A+B Problem

/*\n\n */

int a,b,cs=1;
while(scanf("%d%d",&a,&b)!=EOF){
printf("Case %d: %d\n\n",cs++,a+b);
}

2.每個輸出被空行隔開(最後一個輸出後面不會有空行)

Ex:

    /* Separated */
         
    ...
    int a,b,cs=1;
    while(
    scanf("%d%d",&a,&b)!=EOF){
    if(cs>1)putchar("\n");
    printf("Case%d: %d\n",cs++,a+b);
    }
    ...

string token:

/*
char strtok(char *str,const char *delimiters);
str: 欲切割字串
delimiters: 分隔字符字串
return value: 指向當前切割字串之指標，若切割完畢則回傳NULL
*/

#include<cstring>
...
char str="Welcome to NCKU CSIE. 1*2(3456)78\9";
for( char *token =  strtok( str," \"().*");token!=NULL;token=strtok(NULL," \"().")){
puts( token );
}

	Output
Welcome	to	NCKU
CSIE	1	2
3456	78	9

freopen:

/*freopen*/
...
freopen("f1.in","r",stdin);
freopen("f1.out", "w",stdout);
while(scanf(...)!=EOF){
    printf(...);
}
...

Time complexity and Sorting

###Time complexity

由於競賽題目多有時間限制，我們必須分析程式碼的時間複雜度，根據測資的數量判斷程式大概的執行時間，以避免超過題目的時間限制

𝑶(𝒏):

for(i=0; i<n; i++){
...
}

𝑶(𝒏^2):

for(i=0; i<n ;i++)
    for(j=0; j<n; j++){
     ...
 }

𝑶(𝟐^M):

int two(int n){
    if(n < 2) return 1 << n;
 return two(n - 1)+ two(n - 1);
}
/* maximum n=M */

𝑂(1,000,000) 近似於 1 sec

###Sorting

「排序演算法」

顧名思義就是將一串資料，依照特定的規則排序的演算法。

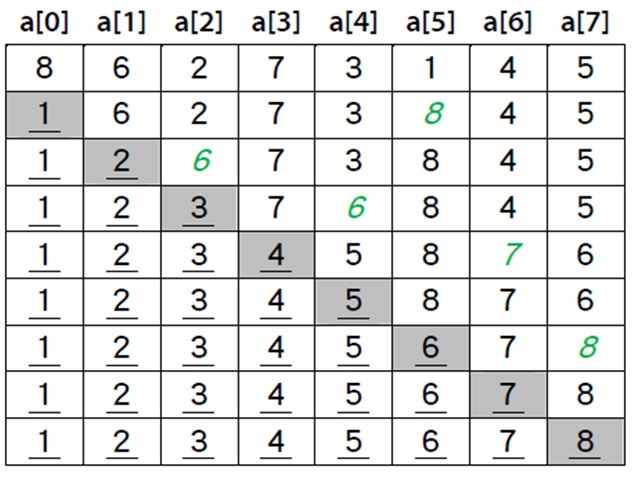
####Selection sort(選擇排序法)

為日常生活中常用到的方法，不斷地找到最小值，再做移動，非常直觀。

時間複雜度為 𝑂(𝑛^2)，且為不穩定排序。

####Bubble Sort

「氣泡排序法」( or 泡沫排序法, 冒泡排序法…) 重複地走訪過要排序的數列，一次比較相鄰兩個元素，如果他們的順序錯誤就把他們交換過來。 時間複雜度 O(n^2)，氣泡排序法為穩定排序。

Stack and Queue