String Basic

string ：有排序的字元集合

substring：一段連續的字串子集合

subsequence：依斷按順序但可不連續的字串子集合

suffix：從後面開始一樣的子字串

prefix：從前面開始一樣的子字串

ex:

String = abcdefg

Substring = “abcd”, “efg”… (連續)

Subsequence = “acdf”, “dfg”…. (不連續)

suffix = “efg”, “defg”….

prefix = “abcd”, “ab”…

Original

方法

兩字串A,B，找出所有B出現在A中的位置，

很直覺的不斷從頭比對，若有字母不符合，則整體再往後退一個，繼續從頭比對

程式碼

for(int i=0; i+lenB<=lenA; ++i)
{
    int mat=0;
    while( mat<lenB && A[i+mat]==B[mat] ) ++mat;
    if(mat == lenB) print(i);
}

簡單的字串比對，時間複雜度為O(|A|)，| |表示字串的長度。

過程請見以下：

• A = “abcdefg”
• B = “cde”

worst case

有可能造成時間複雜度成長為O(|A||B|)

過程請見以下：

• A = “aaaaa….aaa”

• B = “aaaaa….aab”

Hashing

就是幫字串分類到有限數字裡

函數f：string -> {0,1,2….}

• 要求：

1.函數f容易取得

2. 字串分佈均勻，意即碰撞次數愈小愈好

• 思考：

1. f(A) ≠ f(B) ，可以推得 A ≠ B

2. f(A) = f(B) ，可以推得 A = B or A ≠ B (發生碰撞)

3. 若分n類,碰撞機率為1/n

Rabin-Karp rolling hash function

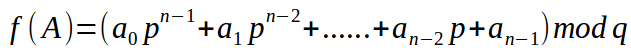
類似p進位制，分成q類(mod q，即對q取餘數)

p,q取不同的質數可讓字串分佈的更加均勻

比對：rolling

以拿A,B兩字串比較為例

1.先計算A所有prefix的hash value,時間複雜度為 O(|A|)

2.可以得出任何子字串的hash value

3.枚舉A長度為 |B| 的子字串,比較hash value,時間複雜度為O(n)

ex:

A = “abcdefg”

B = “cde”

KMP

Knuth-Morris-Pratt algorithm

使用時機： 給定A,B兩字串，尋找B字串是否存在A當中

當B的字串內容，本身有重複的字串時，可用KMP以減少重複否配的時間

ex:

B : aabaab

B字串本身重複 “aab”

方法：先用fail function找出字串B重複的字串

Fail Function

目的：當否配失敗時，能知道字串B要對齊哪裡繼續否配

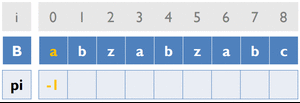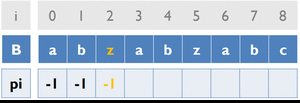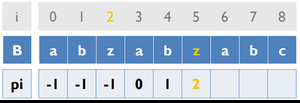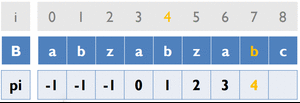
變數：

B [ ] … 存放字串B

pi [ ] … 紀錄前一個重複字串出現的位置

cur_pos … 目前字串重複的位置

初始化：

Z Algorithm

Z_value

從第2個element開始以其為字首，去和以第1個element為首的字串比，找出最長相同字串的長度

Z_Box

最長匹配長度，L表示左邊界，R表示右邊界

如何算出Z_value?

在算Z_value時會有3種case case 1: 自己沒有被別人的Z_Box包住 就乖乖數

L在別人的Z_Box內 i’ 為 i 對應到前綴的位置 (像上面表格的aab(i=5)的a 對應到i=1 的a)

case 2: 若自己的R在剛剛包含自己的Z_Box裏面 ( i’+z[i’] < z[L] => 沒有超過別人Z_Box的右界) 那麼z( i )=z( i’ )

case 3: 若i’+z[i’] >= z[L]代表自己的Z_Box的右邊界和包住自己的Z_Box的右邊界重疊或超過
這時因為無法判斷在包住自己的Z_Box右邊界之後的element情形 所以Z_value只能算到包住自己的Z_Box的右邊界 之後的element都要去一個一個比對

Code

使用方法

當要看B字串是不是A的子字串時，用一個沒有出現過的符號放在兩者之間， 並用Z algorithm，若A字串內的字元有Z_value等於B的長度，即B出現在A裡面