版本 7b7bcd6401311f2861449bf40a04a9d711ee026a

acm/course/MST

#MST (Minimum Spanning Tree, 最小生成樹) ##Spanning Tree (生成樹) 1. 一棵包含圖上所有點的樹，稱作該圖的生成樹

一張圖的生成樹可能會有很多種
完全連通圖才有生成樹 (不連通時，則稱為生成森林)
生成樹的權重為樹上每條邊的權重總和

##Minimum Spanning Tree 擁有最小權重的生成樹，稱為最小生成樹

###Kruskal’s Algorithm (greedy based) 1. 依照權重排序

選擇較小的邊，並檢查是否有環

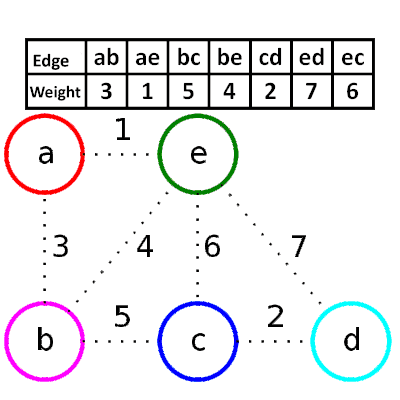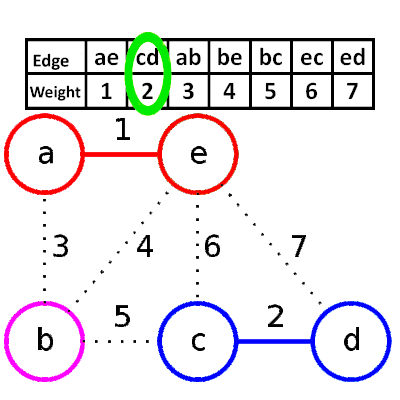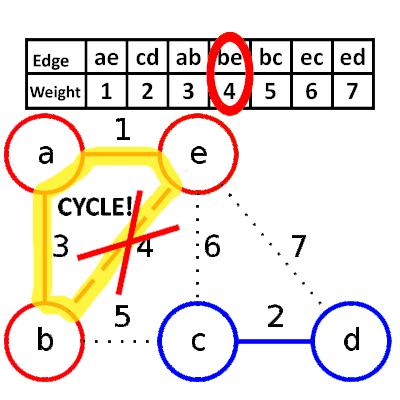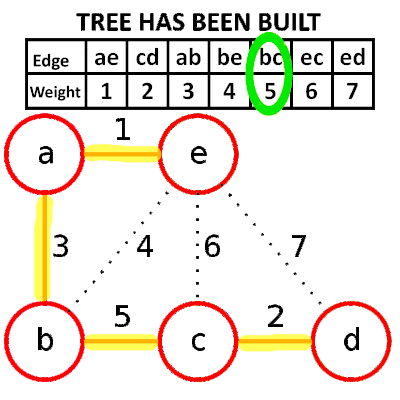
Psuedocode

KRUSKAL(G):
 A = ∅
 foreach v ∈ G.V:
    MAKE-SET(v)
 foreach (u, v) in G.E ordered by weight(u, v), increasing:
    if FIND-SET(u) ≠ FIND-SET(v):
       A = A ∪ {(u, v)}
       UNION(u, v)
 return A

時間複雜度 O(ElgE)

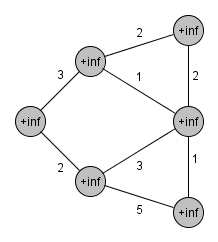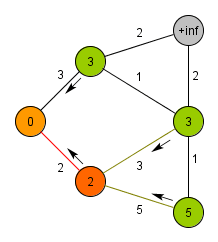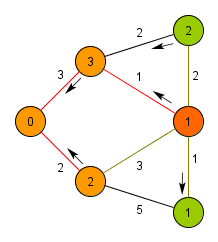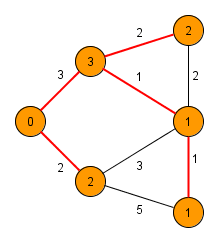
###Prim’s Algorithm (relaxation based) 1.所有節點設為未拜訪過 (設為INF)

2.令d[i]為到節點i的距離(每次皆考慮鄰近節點)

3.考慮所有鄰近樹且未拜訪過的節點i，選擇距離最近的節點，並檢查是否有環

4.更新拜訪過節點與鄰近節點d[i]

int w[9][9];    // adjacency matrix
int d[9];       // 紀錄目前的MST到圖上各點的距離
int parent[9];  // 紀錄各個點在MST上的父親是誰
bool visit[9];  // 紀錄各個點是不是已在MST之中
 
void prim(){
    for(int i=0; i<9; i++)	visit[i] = false;
    for(int i=0; i<9; i++)	d[i] = 1e9;
 
    d[0] = 0;   // 可以選定任何點作為樹根，這裡以第零點作為樹根。
    parent[0] = 0;
 
    for(int i=0; i<9; i++){
        int a = -1, b = -1, min = 1e9;
        for(int j=0; j<9; j++)
            if(!visit[j] && d[j] < min){
                a = j;  // 記錄這一條邊
                min = d[j];
            }
 
        if(a == -1)	break; // 與起點相連通的MST都已找完
        visit[a] = true;
//      d[a] = 0;           // 註解後，得到MST每條邊權重。
 
        for(b=0; b<9; b++)
            if(!visit[b] && w[a][b] < d[b]){
                d[b] = w[a][b]; // 離樹最近，不是離根最近。
                parent[b] = a;
            }
    }
}

*時間複雜度 O(𝑉")

With Binary-Heap : O( (V+E)logV)

參考來源：

演算法筆記 http://www.csie.ntnu.edu.tw/~u91029/SpanningTree.html

維基百科 https://en.wikipedia.org/wiki/Kruskal%27s_algorithm