版本 73f4b1a9c53b47ca020acf43e1ce7bc7abddd055
acm/course/String_Matching
KMP
Knuth-Morris-Pratt algorithm
使用時機: 給定A,B兩字串,尋找B字串是否存在A當中
當B的字串內容,本身有重複的字串時,可用KMP以減少重複否配的時間
ex:
B : aabaab
B字串本身重複 “aab”

方法:先用fail function找出字串B重複的字串
Fail Function
目的:當否配失敗時,能知道字串B要對齊哪裡繼續否配
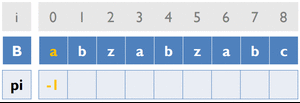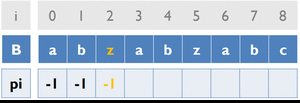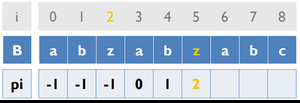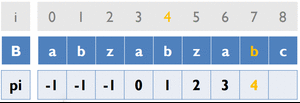
變數:
B [ ] … 存放字串B
pi [ ] … 紀錄前一個重複字串出現的位置
cur_pos … 目前字串重複的位置
初始化:
![cur_pos 初始為 -1 pi[0] 初始為 -1](/acm/KMP_3.gif)
Z Algorithm
Z_value
從第2個element開始以其為字首,去和以第1個element為首的字串比,找出最長相同字串的長度

Z_Box
最長匹配長度,L表示左邊界,R表示右邊界

如何算出Z_value?
在算Z_value時會有3種case case 1: 自己沒有被別人的Z_Box包住 就乖乖數

L在別人的Z_Box內 i’ 為 i 對應到前綴的位置 (像上面表格的aab(i=5)的a 對應到i=1 的a)
![Z_value[5]=Z_value[1]](/acm/case2.gif)
這時因為無法判斷在包住自己的Z_Box右邊界之後的element情形 所以Z_value只能算到包住自己的Z_Box的右邊界 之後的element都要去一個一個比對
![for a(i=9) its Z_value is 2 ,differ from Z_value[1]](/acm/case3.gif)
Code

使用方法
當要看B字串是不是A的子字串時,用一個沒有出現過的符號放在兩者之間, 並用Z algorithm,若A字串內的字元有Z_value等於B的長度,即B出現在A裡面

