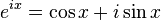Sampling Theorem 證明
- 訊號轉換公式
- 類比訊號如何用數位的形式放到電腦記憶體中?
- 公式: X[n]=X(nTs)
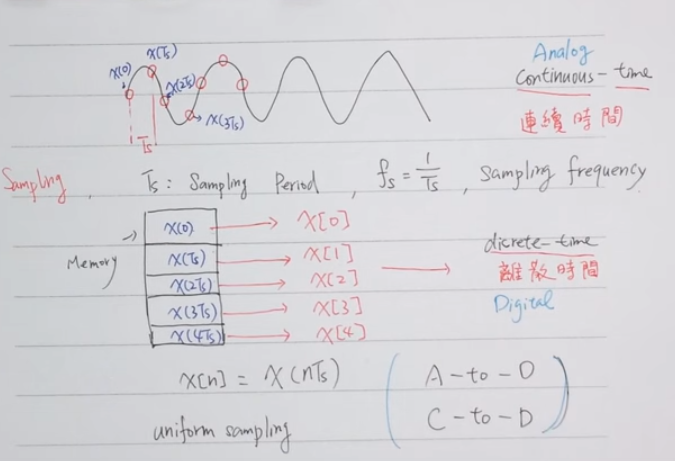
- 連續弦波的表示式
- 取樣頻率多少才夠?
- 直覺想法:
一個周期至少要有
波峰、波谷,你才有機會重現原來的波形,只取一個點會變成直流
- 數學推導
- 先了解aliasing現象,也就是取樣頻率不夠的時候會怎麼樣
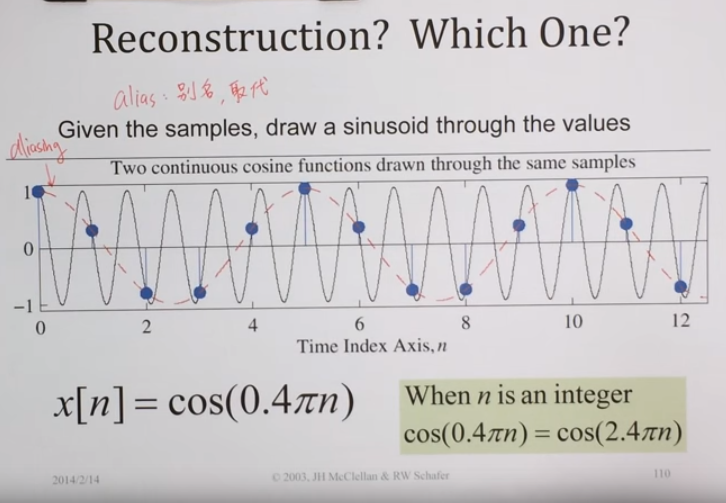
- alias: 別名(n)、取代(v)
- 取樣頻率低於2倍最高訊號頻率而導致失真、原先的弦波被錯誤的取樣弦波取代,這個現象稱為aliasing
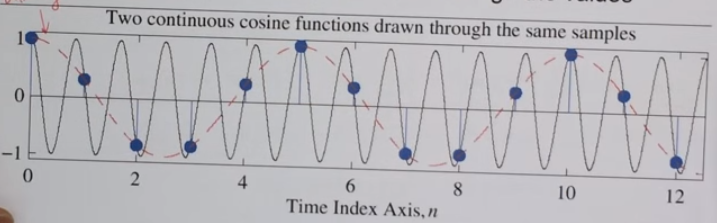
- 以下圖為例,原先的弦波被紅色的弦波給取代掉(EX:歌聲男聲女聲)
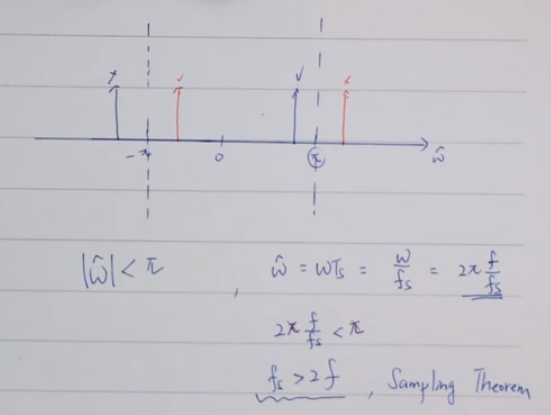
- Sampling Theorem(Shannon sampling theorem)
- 取樣頻率多少才夠? 兩倍以上才不會失真、才不會被取代掉
- Depends on frequency of Sinusoid(弦波)
- X(t), fmax( X(t)裡面最高的頻率 )
- X[n] = X(nTs)
- fs = 1/Ts > 2fmax
- 當取樣頻率為原訊號之最高頻率之兩倍以上時,才可以正確的重建原始訊號
- 用 Discrete-Time Sinusoid
- 主要講 ω hat: digital frequency的概念

- EX: 100Hz 用 1000 Hz 取樣
- 可以劃出頻譜
- cos 裡面住著兩個 exponential,一個在正,一個在負
- 0.2 pi 有一個 pick, -0.2 pi 也會有一個 pick
- 強度就是 Aejφ /2 、 -Aejφ /2

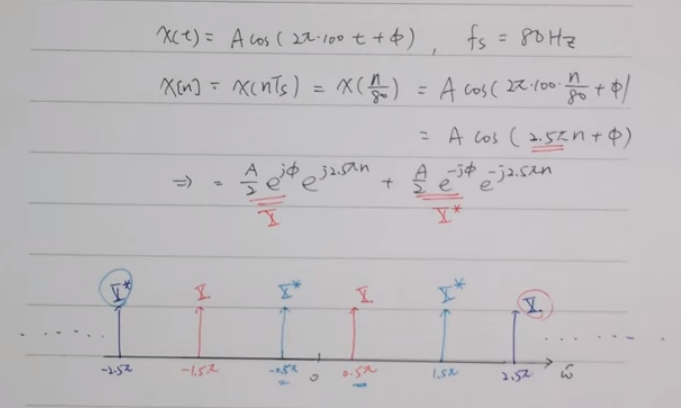
- EX: 100Hz 用 100Hz 取樣
- 中間有一段是透過Euler’s formula做轉換
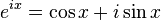

- 產生 aliasing,無法辨認
- 數位的頻譜和類比的頻譜就是有很多 alias
- 每個 2 pi 都會有一個alias
- 強度一樣是 Aejφ /2 、 -Aejφ /2
- 電腦會重建最低的頻率,王力宏(男聲) v.s. 張惠妹(女聲)


- 要取的頻譜要是alias中頻率最低的
- 100 取 1000

參考資料來源